type
status
date
slug
summary
tags
category
icon
password
题目:判断二分图
存在一个 无向图 ,图中有
n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。给你一个二维数组 graph ,其中 graph[u] 是一个节点数组,由节点 u 的邻接节点组成。形式上,对于 graph[u] 中的每个 v ,都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性:
• 不存在自环(graph[u] 不包含 u)。
• 不存在平行边(graph[u] 不包含重复值)。
• 如果 v 在 graph[u] 内,那么 u 也应该在 graph[v] 内(该图是无向图)
• 这个图可能不是连通图,也就是说两个节点 u 和 v 之间可能不存在一条连通彼此的路径。
二分图 定义:如果能将一个图的节点集合分割成两个独立的子集
A 和 B ,并使图中的每一条边的两个节点一个来自 A 集合,一个来自 B 集合,就将这个图称为 二分图 。
如果图是二分图,返回 true ;否则,返回 false 。示例 1:
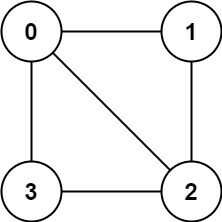
示例 2:
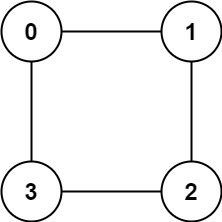
提示:
graph.length == n
1 <= n <= 100
0 <= graph[u].length < n
0 <= graph[u][i] <= n - 1
graph[u]不会包含u
graph[u]的所有值 互不相同
- 如果
graph[u]包含v,那么graph[v]也会包含u
题解
要判断一个无向图是否为二分图,我们可以采用
染色法。基本思路是给每个节点分配两种颜色之一,使得没有两个相邻的节点拥有相同的颜色。如果能够以这种方式成功地为图中的所有节点着色,那么这个图就是二分图。实现步骤如下:初始化一个数组
colors 来存储每个节点的颜色。0 值表示节点尚未着色,1 和 -1 将代表两种不同的颜色。
遍历每个节点。如果节点未着色,则用一种颜色(比如 1)着色,然后使用深度优先搜索(DFS)或广度优先搜索(BFS)为所有相邻节点着上另一种颜色(-1)。
在 DFS 或 BFS 过程中,如果发现一个相邻节点已经被着上了与当前节点相同的颜色,则图不能被划分为二分图,返回 false。
如果成功为图中的所有节点着色而没有冲突,返回 true。
以下是使用
BFS 实现的 JavaScript 代码示例:附录
- Author:Zinphy
- URL:https://zouysay.cn/article/660e20f8-26ae-4069-9a80-b019236bd108
- Copyright:All articles in this blog, except for special statements, adopt BY-NC-SA agreement. Please indicate the source!